孔尺度模型是一个功能强大的数值工具，已经被广泛用于观测复杂微观结构内的介观尺度现象与燃料电池的电极开发。然而，因为孔尺度模型自身的计算时间步长过小（1e-8 s量级），所以无法被用于模拟长时间的瞬态过程。因此，孔尺度模型一直没有被用于进行燃料电池电极内衰减过程的研究，而电极在衰减过程中内部发生的变化对于电极的开发是非常有价值的，如何同时拥有介观的模拟尺度和时间尺度上的分析，这是一个有趣的科研问题。

 

在我们组与德国Fraunhofer ISE研究所最近合作的工作中，受到数学中积分思路的启发，提出了一种迭代算法可以将孔尺度模型运用在时间尺度分析，这种思路可以扩展孔隙尺度模型在科学和工程中的应用。

具体实现思路如下：

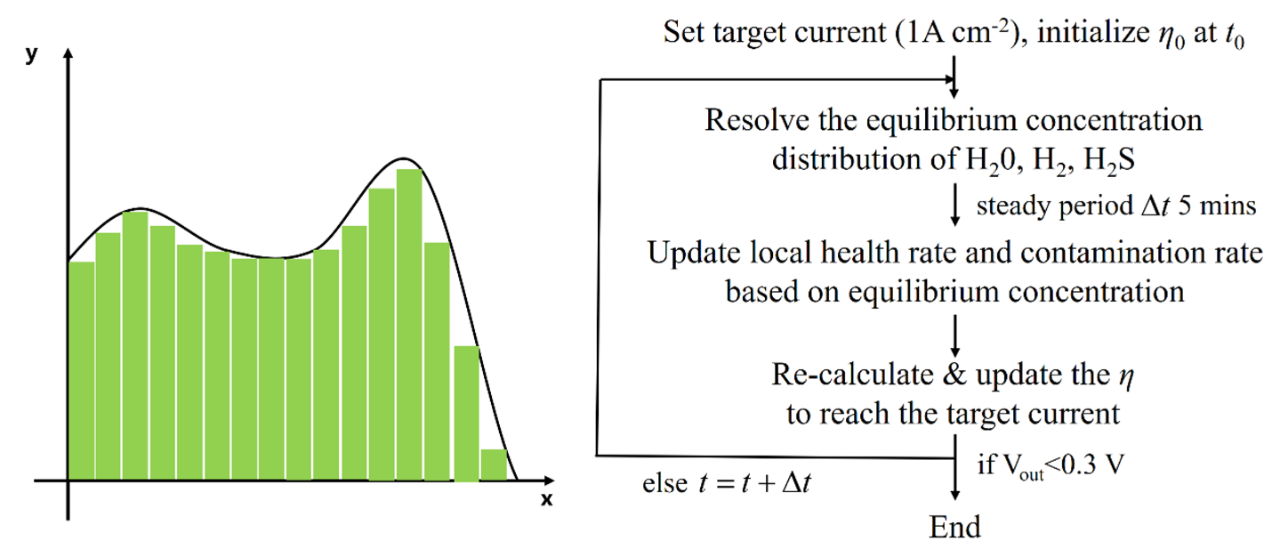
对于求解曲线的积分面积，数学积分的思路将其分解为无数个规则的矩形去逼近其原本的形状，通过累加矩形的面积可以近似得到曲线的积分面积。在本工作的算法中，为了实现时间尺度的模拟，我们将整个电极衰减的过程同样离散为很多时间段；假定每个时间段内，电极为稳态运行，通过孔尺度模型对其求解；模拟稳定后，根据该时间段模拟结果决定下个时间段电极内的边界调节。以下为模拟数据与时间数据的对比：

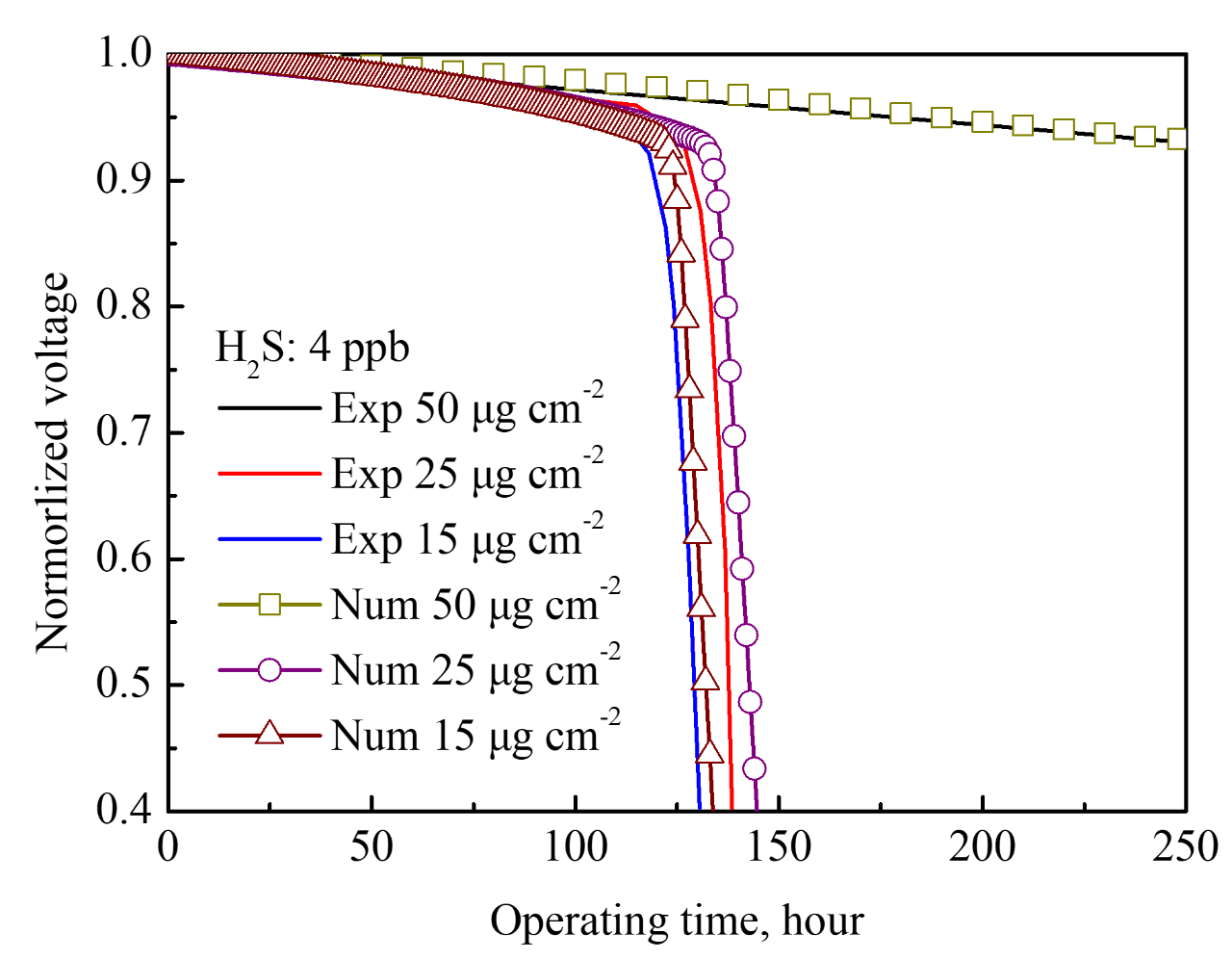
催化层在4ppb硫化氢污染下性能衰减对比

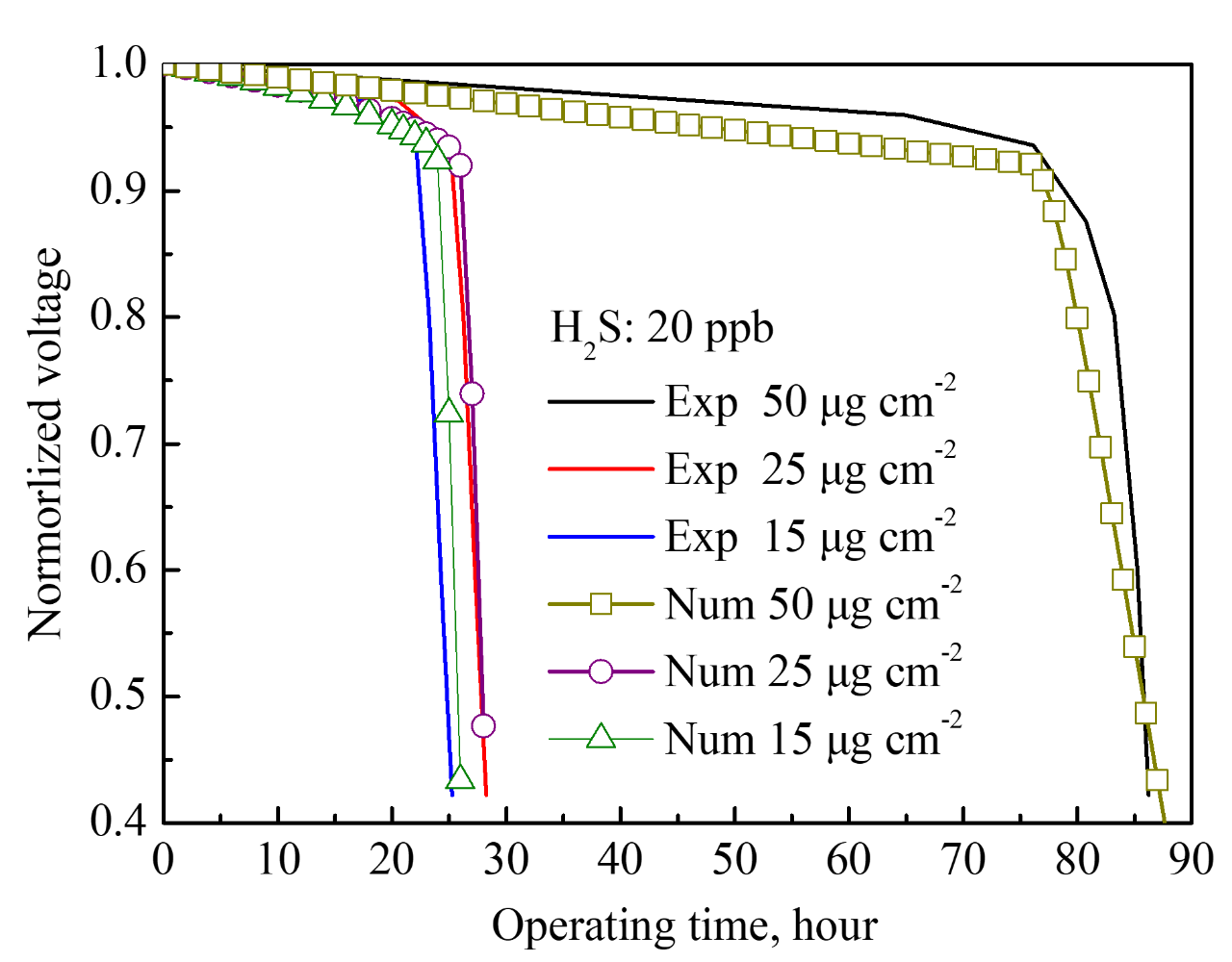
催化层在20ppb硫化氢污染下性能衰减对比

需要注意的是，这种算法的精准度取决于设定时间段的长度和整个瞬态过程的变化激烈程度。如何从根本上突破模型物理与时间尺度的限制，未来还需要更多的投入。

本工作还具体讨论了电极铂载量，硫化氢及其不同浓度对于电极耐久的影响。更多细节请参见原文：

https://link.springer.com/article/10.1007/s12678-021-00664-9