用于实时仿真的1+1维多相质子交换膜燃料电池模型

原文链接：

https://doi.org/10.1109/TTE.2021.3115794

前言

质子交换膜燃料电池被认为是未来清洁运输的一种非常有前景的能量转换装置。尽管如此，成本和耐久性仍然是制约PEMFC商业化的重要因素。为确保燃料电池在不同功率要求下的快速响应和稳定运行，有必要设计合适的燃料电池管理策略，使燃料电池具有更高的发电效率和更长的系统寿命。根据上述的要求，因此非常需要再硬件在环（HIL）系统中构建PEM燃料电池实时模型。这种实时模型旨在维持最佳运行条件并改善燃料电池系统的整体性能。在燃料电池控制策略验证和燃料电池系统辅助设备设计测试的初始阶段，实时模型可用于在HIL系统中替换真实对象，而不会对燃料电池组造成任何风险。本研究建立了1+1维的质子交换膜燃料电池（PEMFC）多相模型，并模拟了燃料电池在各种工况下的动态特性。该模型耦合了电化学、流体和热物理现象，能够准确描述质子交换膜燃料电池内部的多种物理过程。同时，该模型还考虑了水的相变和氮的交叉。所建立的模型可以应用于燃料电池在常温和冷启动工况。除此之外，讨论了模型中时间步长的选择，提出了实时模型的求解方法。通过简化膜电极组件（MEA）内的多组分扩散，大大提高了计算效率，从而使计算时间比模拟物理时间更短。该模型适用于实时仿真或在线诊断控制等嵌入式应用。通过比较稳态、负载变化和冷启动等各种工况下的极化曲线、欧姆电阻、局部电流密度分布和电压演变等仿真结果，进行了综合模型验证，保证了模型的准确度。最后，通过仿真实例进一步验证了模型的仿真能力。

 

研究方法

本研究中的计算域如图1所示。该模型的结构包括流道、气体扩散层、微孔层、催化剂层和质子交换膜。为了进一步提高计算效率，将GDL、MPL和CL结合起来简化流场，忽略了组分在多孔层内的扩散。该模型以垂直膜为主要方向，沿通道划分多个节点，形成1+1维燃料电池模型计算域，从而反映上下游的分布情况。此外，模型耦合电化学、流体和热三个物理场，可以有效地计算PEMFC在瞬态过程中的气体组分输运、产热和电密度分布。此外，该模型还考虑了水的相变、氮在膜上的传输和冷启动条件。

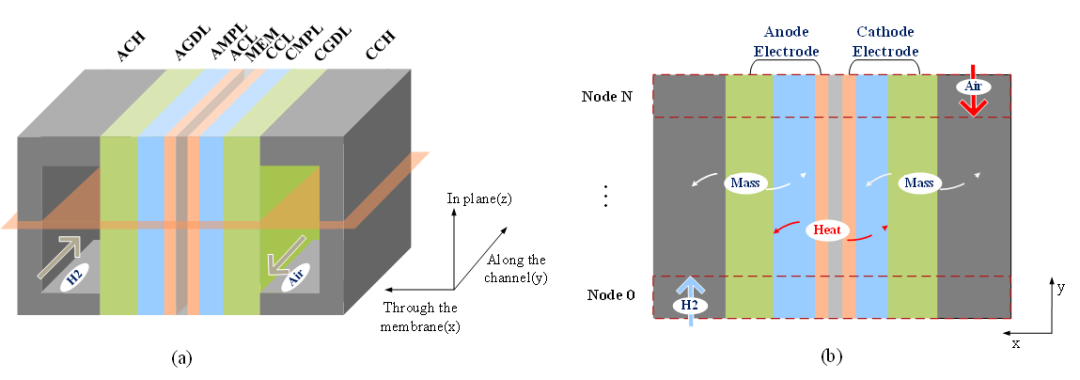
图1 质子交换膜燃料电池实时模型计算域示意图

模型求解采用离散控制方程的显式格式，为了避免发散，又保证计算精度，时间步长选择为10-4s。在计算过程中，物理量每10-2s（100个时间步）输出一次。时间步长较大可以使模型具有较高的计算效率，满足实时性要求。然而，在模型流体扩散的求解过程受时间步长的限制，较大的时间步长可能导致模型的发散。此前研究的数值结果中阐明了显式格式的不稳定发散的原因是由时间步长过大引起的，并针对二维扩散方程提出了显式格式的稳定性条件，当时间步长满足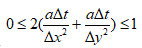要求，数值结果将收敛。时间步长计算选取为10-4s，这是该模型数值计算的稳定条件。从而提出了一套实时模型的时间步长选择和效率优化方法，使模型在收敛条件下达到实时计算效率要求，具体选择方法如图2所示。该电堆模型在2.4Ghz处理器的计算机上的计算效率是实时效率的2-3倍，未来可进一步扩展以实现系统级层面。

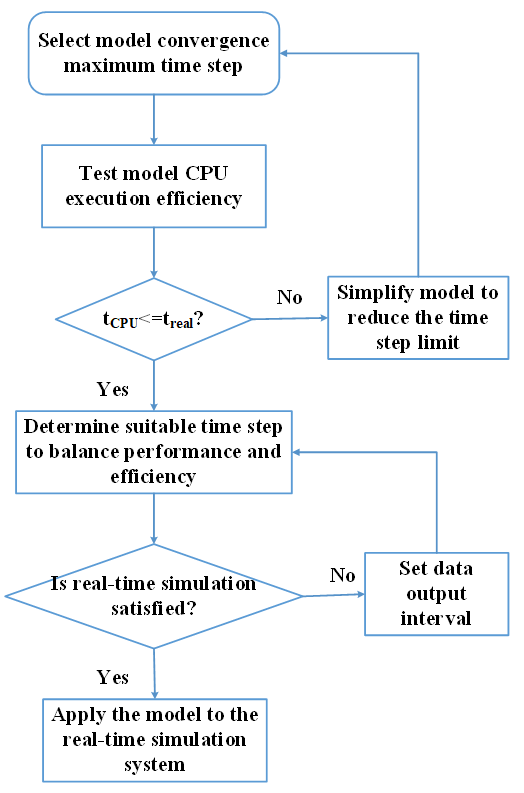
图2 实时仿真的时间步长选取方法

如图3（a）所示，模型已完成网格独立性验证，结果表明，节点数N=5和N=10之间的输出电压和电流密度分布差异不大。考虑到计算效率，模型沿流道方向节点设为5更适用于计算。另外为了验证模型的准确性，本研究将模型的模拟结果与稳态极化曲线、冷启动过程、沿流道的电流密度分布和动态变负载四种不同类型的实验数据进行了比较。通过这些验证，证明所提出的实时模型能够以非常高的精度预测燃料电池的性能。稳态极化曲线：将模拟结果与两组不同条件下的实验数据进行比较。如图3（b）（c）所示，在不同的阴极加湿（66%和100%）下，输出电压和欧姆电阻与实验数据基本一致，模拟与实验的平均误差率约为4.4%。图4（d）（e）显示验证了另一组不同阳极和阴极增湿的极化曲线实验数据，平均误差率约为3.1%，燃料电池温度为343.15K，化学计量比设置为1.5，阳极/阴极入口流速设置为0.5/1.5 SLPM。通过两组不同工况下的实验数据验证了该模型对输出性能预测的准确性。

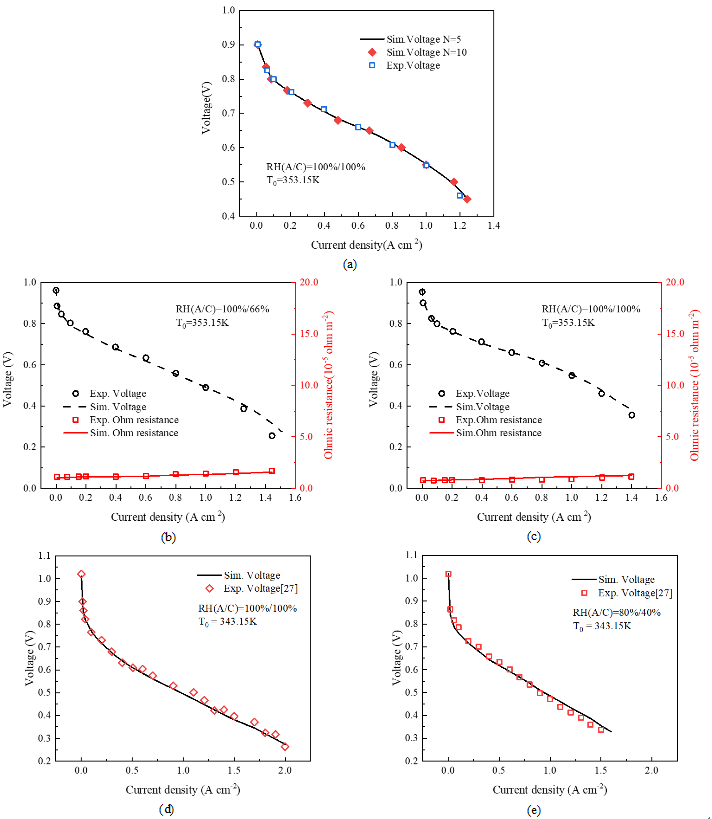
图3 模型验证——稳态极化曲线与欧姆阻抗

冷启动过程：目前应用于HIL系统的电堆实时模型几乎没有考虑冷启动工况，但冷启动其实是限制燃料电池广泛应用的重要原因之一。本研究将模拟结果与冷启动过程的三组实验数据进行了比较，验证了模型冷启动过程的合理性。同时，实验数据和模拟结果表明，随着膜初始含水量的增加，冷启动过程的持续时间缩短。初始膜含水量与不同的吹扫策略有关，气体吹扫旨在清除燃料电池中的水，从而避免在冰点温度下导致内部结冰和堵塞。另外如图4（c）（d）所示，欧姆损耗也受含水量的影响，欧姆损耗将随着含水量的增加而减小。此外，冷启动性能受初始温度的影响，这可以从图4（b）和图4（c）（d）之间的比较中得出。温度越低，结冰速度越快，冷启动更容易失败。

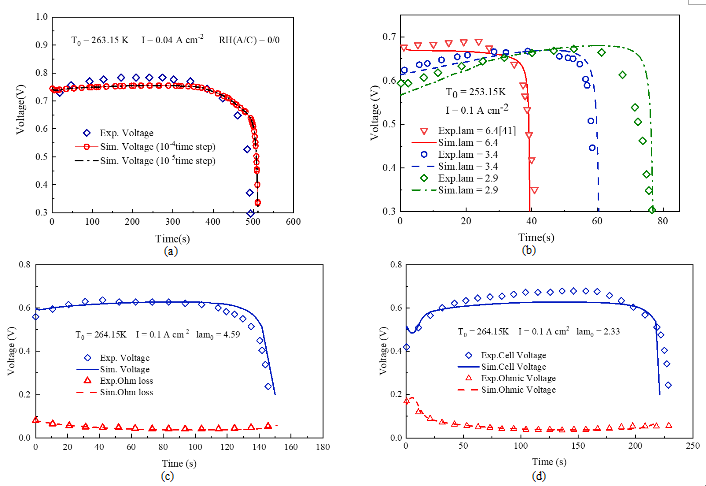
图4 模型验证——冷启动过程

电流密度分布：电流密度分布的预测模拟结果与洛斯阿拉莫斯国家实验室的实验数据进行了比较。实验数据是在三种不同的启动电流密度（0.1 A cm-2/1.0 A cm-2/1.2 A cm-2）下获得的，电流密度分布数据沿流道分为5个节点得到。图5表明，实验和模拟结果显示了相似的电流密度分布。上游电流密度远高于下游电流密度，与实验数据一致。三组模拟结果与实验数据之间的最大绝对误差不超过0.15 A cm-2，对于不同启动电流密度的三组，平均绝对误差分别为0.0136 A cm-2、0.062 A cm-2和0.038 A cm-2。平均相对绝对误差为7%，在允许范围内。

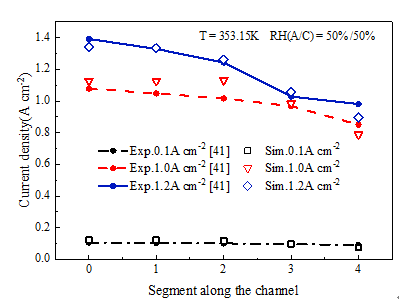
图5 模型验证——电流密度分布

循环负载工况的动态响应：如图6表明，与实验数据相比，燃料电池电压动态变化的仿真结果具有极高的准确度，证实了该模型预测动态响应性能的能力。同时，当电流密度突然上升或者下降时，输出电压会首先下降到最小值或上升到最大值，然后逐渐恢复到相对稳定的状态，表现出明显的电压下冲和过冲现象。这种现象主要是由于当电流密度突然升高时，增强的电渗阻力作用会导致膜在短期内脱水，导致燃料电池欧姆电阻在短期内增加。随后，阴极产生的水通过反向扩散润湿膜，从而降低欧姆电阻。此外，随着阶跃电流密度的增加，电压下冲和过冲现象也会更加明显。

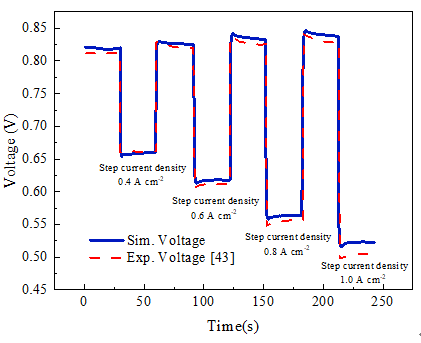
图6 模型验证——循环负载工况的动态响应

除此之外，在研究工作的后半段，通过仿真实例进一步验证了该模型的预测能力。分析了燃料电池沿流道的空间分布特性和阳极组件的变化特性，研究了低入口湿度下工作温度对电池性能的影响。