


实现质子交换膜燃料电池动态过程实时优化:采用半循环滑动窗口的数据驱动方法

https://www.sciencedirect.com/science/article/pii/S0306261921010230
质子交换膜燃料电池(PEMFC)的可靠性与动态运行过程中合适的运行条件密切相关。本研究提出了一个动态过程控制策略优化框架,通过机器学习方法以确定PEMFC冷启动的最佳控制策略,提高电池冷启动能力并缩短启动时间。研究了不同初始温度下恒流和动态电流对PEMFC冷启动的影响。开发的PEMFC动态模型的数值结果表明,在冷启动时间方面,恒流斜率策略(CCSS)比恒流策略(CCS)更有效。在CCSS研究中,过大的电流斜率会导致电压下冲,进而导致冷启动失败,而过小的电流斜率会导致在研究的工作条件范围内启动过程较长。通过半循环滑动窗口(Semi-recurrent sliding window)方法结合人工神经网络(ANN)和仿真数据,开发了一种数据驱动动态预测模型,用于冷启动期间的动态预测和实时优化。基于此NN-SW模型,已经确定了CCSS下特定的安全临界运行条件曲线。进一步提出了实时自适应控制策略(RACS),以优化PEMFC冷启动期间各种初始温度的工作电流。与最佳CCSS相比,RACS被证明对于PEMFC冷启动启动更加稳健和高效。基于RACS,初始温度为-20°C的启动时间可以减少26.7%。此外,还测试了NN-SW模型对冰的预测,结果令人满意,测试结果的平均决定系数为0.9773。
本文提出一种基于数据驱动的燃料电池动态过程操作条件优化框架,采用改进半循环滑动窗口方法建立数据驱动模型,实现燃料电池冷启动过程快速预测和实时优化,研究操作条件的影响并针对冷启动过程特点进行优化。首先基于之前开发的燃料电池动态模型,探讨了运行电流密度对燃料电池性能的影响,包括冷启动过程中的温度和启动最终状态,通过调查确定最佳恒定电流加载速率的存在。在本文中,电池启动成功和较短启动时间都是冷启动策略优化的目标,为了进一步提高燃料电池冷启动能力,缩短低温启动时间,需要根据基于电流加载速率策略(Constant current slope strategy,CCSS)进一步确定操作条件安全范围。因此,开发了采用改进的滑动窗口方法耦合神经网络和线性回归两种机器学习方法的数据驱动模型。在数据驱动模型的设置中还充分考虑了积冰对燃料电池性能的影响。此外,还针对模型的预测能力和泛化能力进行了精度验证和K折交叉验证。训练后的模型可以预测各种动态电流下的电池电压和温度,并将操作条件与启动时间相关联。提出基于数据驱动模型的实时自适应控制策略(Real-time adaptive control strategy,RACS),缩短了启动时间和原始策略的鲁棒性,优化后的操作条件通过数值模型验证确认该策略的可靠性。
本研究中质子交换膜燃料电池冷启动优化方案的工作流程如图1所示。首先,通过实验结果验证开发的准二维燃料电池动态模型,然后基于该模型研究了燃料电池冷启动的两种电流控制策略。随后,通过数值模拟中生成的数据进行训练机器学习方法,然后与半循环滑动窗口方法相结合,以实现燃料电池冷启动启动中的动态预测和实时控制。数据驱动模型在预测准确性和泛化方面得到了很好的测试。最后,基于数据驱动模型确定了恒电流加载速率策略下燃料电池冷启动的最佳操作条件,通过提出的实时自适应控制策略进一步改进原始恒电流加载速率策略。
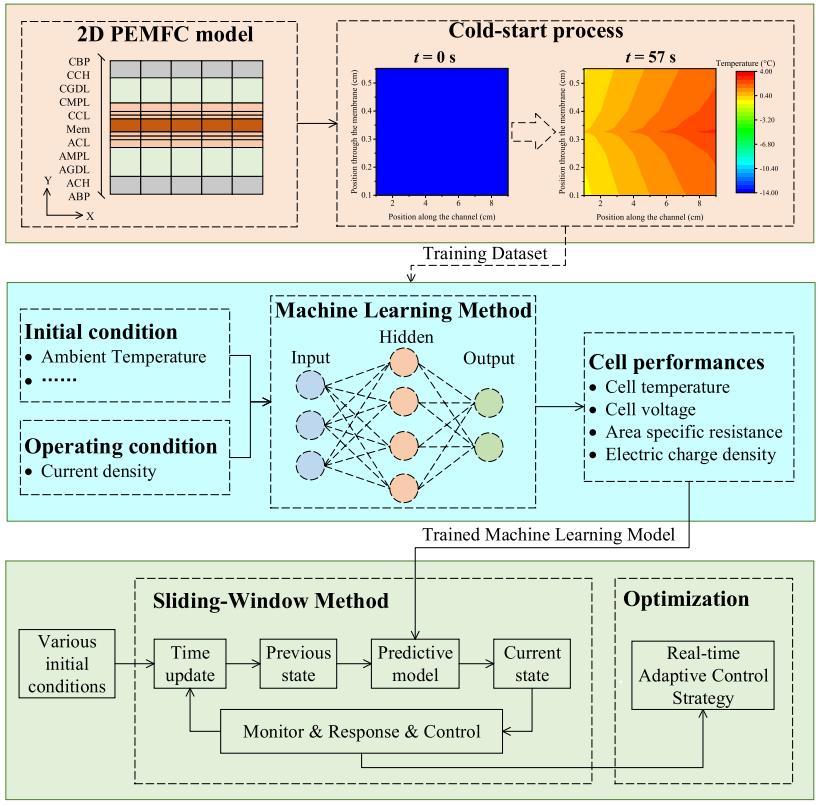
图1 动态过程控制策略优化框架
图2展示数值模型预测冷启动过中输出电压和温度与实验结果的比较,验证动态模型的可靠性。模型的操作条件均与冷启动实验中的操作条件保持一致,其他未知参数设定为燃料电池的典型值。比较结果显示,模型仿真与实验策略数据匹配良好,输出电压和温度的根方根误差(Root mean squared error, RMSE)分别为0.0344 V和0.6079 °C,这表明模型的预测结果是可靠的。
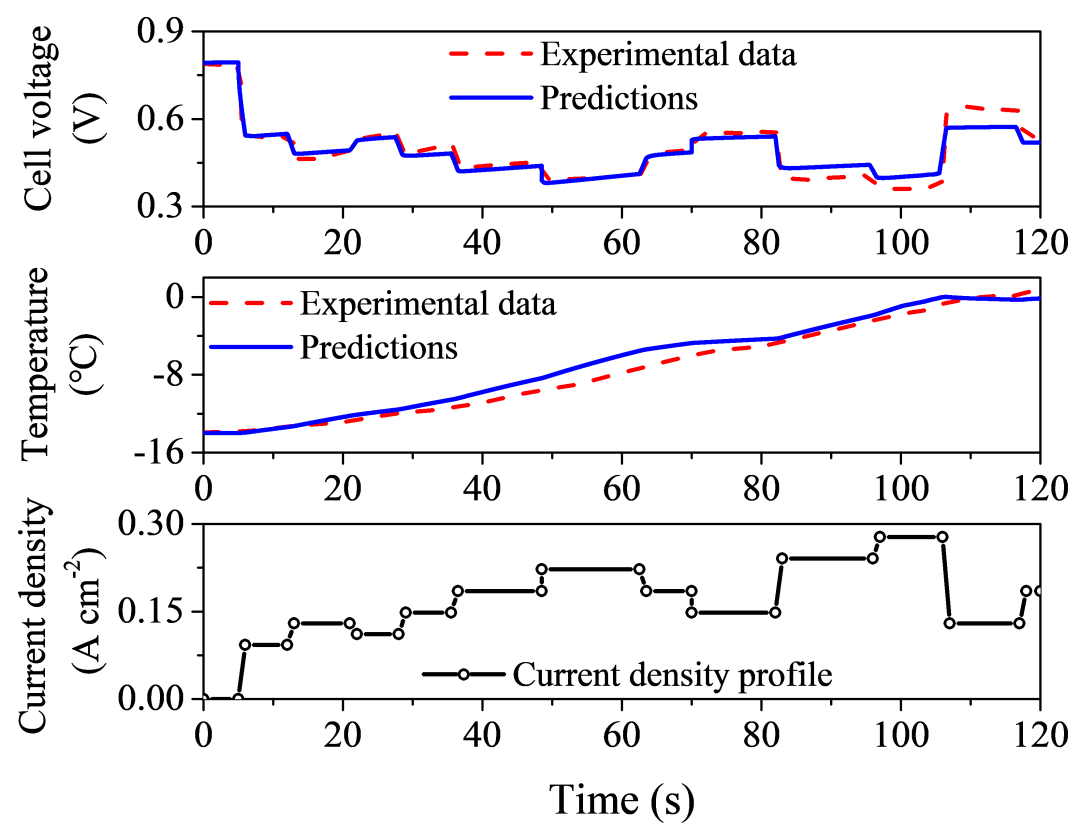
图2 变载荷启动过程模型预测和实验数据对比
随后基于数值模型生成了12组不同初始条件和边界条件的冷启动过程,总结如表1。电池温度和电压变化如图3所示。
表1 不同初始条件和边界条件的冷启动
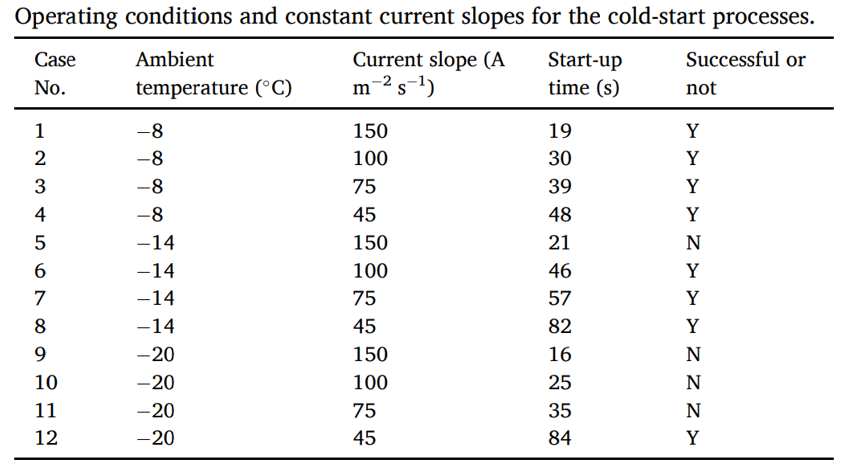
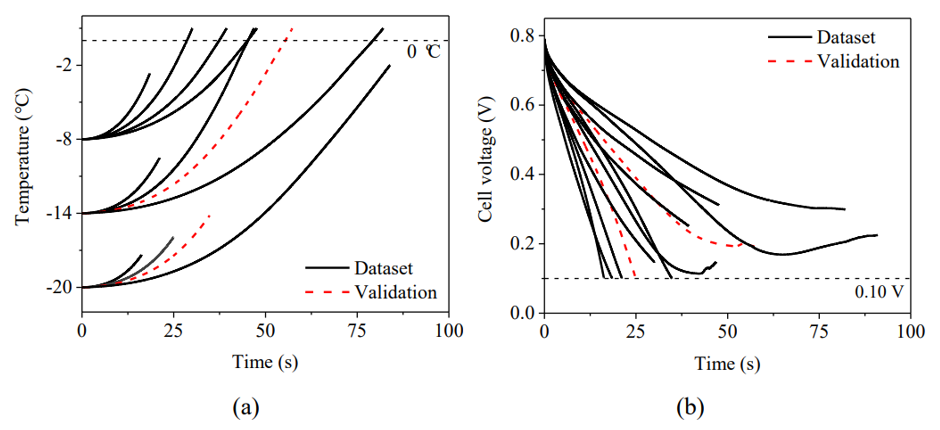
图3 仿真冷启动数据集:(a) 温度变化;(b) 输出电压变化
滑动窗口方法广泛应用于机器学习方法处理时间序列数据,因为它可以将序列监督学习问题转化为传统的监督学习问题。图4 (a)显示了典型的滑动窗口方法预测流程图。滑动窗口方法最典型的特征是将序列数据成段分入随时间滑动的窗口,每个窗口里的数据进一步分为输入X和输出Y。滑动窗口的的宽度表示输入X和输出Y共同涉及的时间层数。需要注意的是,在典型滑动窗口方法中,窗口中的输入X和输出Y在数据本身没有交集,它们共同组成机器学习方法的训练集或测试集中的一个样本。通过这种方式,传统的监督学习机器学习方法,比如人工神经网络或者线性回归等,可通过耦合滑动窗口方法预测时间序列数据。值得注意的是,训练集组成不直接受序列数据的影响,可以由来自不同动态过程的数据组成,这对于工程问题的实际应用非常重要。虽然这种典型的滑动窗口方法可以在许多应用中做出合理的预测,但它需要在预测输出Y之前提前获取输入X的整个序列的数据。更确切地说,如果某些输入X在特定时间步骤中丢失或未知,那么耦合典型滑动窗口方法的机器学习模型将无法继续预测新的输出Y。因此,这种典型的滑动窗口方法实际上不适合应用于燃料电池冷启动预测,因为冷启动过程的输入X,比如温度,在初始时刻之后的动态过程中都是未知的。
为了克服上述限制,学者对这种滑动窗口方法进行改进,即循环滑动窗口(Recurrent sliding window)方法,其工作流程图显示在图4 (b)。循环滑动窗口方法的主要特征是,前一个时间层或前多个时间层(取决于时间窗口宽度)的输出Y作为当前时间层中的输入X,当机器学习模型预测新输出Y后,重新更新下个时间步的输入。通过这种改进,机器学习模型可以根据初始的输入X不断预测未来的输出Y。事实上,循环滑动窗口方法可以解决大多数受初始条件影响的动态预测问题。然而,基于循环滑动窗口方法的数据驱动模型在除初始时刻外,动态预测过程中所有的输入X均由上一步的预测值给出,这导致数据驱动模型将无法考虑动态过程中操作条件变化的影响,比如操作电流变化对冷启动过程的影响,极大限制了数据驱动模型在变工况动态过程中的应用。
为了解决上述问题,本节将介绍一种半循环滑动窗口(Semi-recurrent sliding window)方法,其输入由之前时间层里的数据X1和当前时间层的数据X2共同组成(图4 (c))。其中X2仅包含操作参数,比如冷启动过程中的操作电流密度。通过这种改进,半循环滑动窗口方法不仅保留了用于预测动态过程的能力,还可以在每次预测前,通过人为调整输入X2实现对动态过程的调整。为了解决初边值问题,确保预测模型可以从初始时刻开始模拟,在本研究中时间窗口的宽度默认设置为2,即每个窗口内通过上一个时间层的数据预测当前时间层中未知的数据。
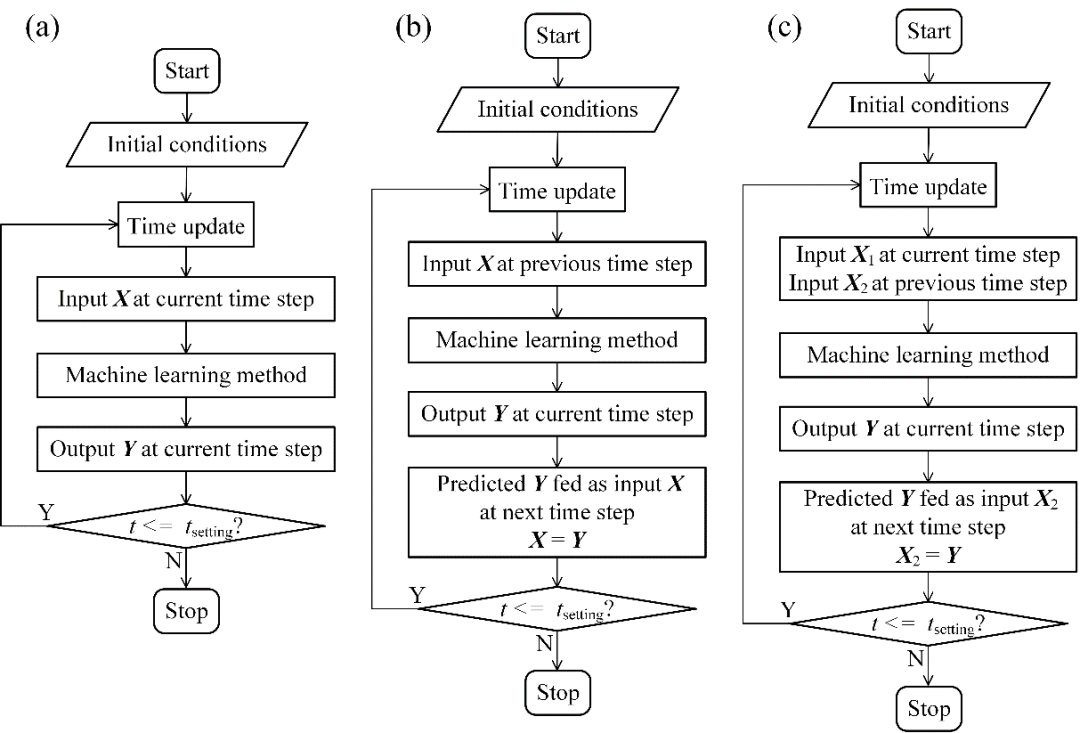
图4 基于滑动窗口方法的机器学习方法预测流程图:(a) 典型滑动窗口;(b) 循环滑动窗口;(c) 半循环滑动窗口
数据对于机器学习模型的预测能力起到决定性作用。考虑到当前实验测量技术的能力,燃料电池冷启动实验中可直接测量4个变量分别是电池电压(Vout, V)、电流密度(I, A cm-2)、极板温度(T, °C)和面电阻(ASR, Ω cm2)。值得注意的是,目前催化层中冰的饱和度是不可测量的。根据其他学者完成的工作,电池冷启动期间电化学反应产生的总水量与水的其他相密切相关,如膜态水、过冷水和冰,而冰对电池冷启动过程有重大影响。因此,定义变量电荷密度(Qg,C m−2)作为数据驱动模型的第5个输入变量,为机器学习方法提供有关结冰的信息。每个时间步的电荷密度计算如下:
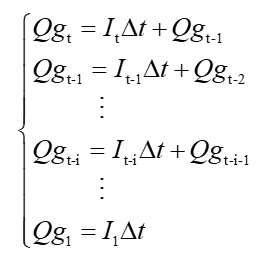
其中Δt是时间步长(s),It是当前时间层的操作电流密度。显然,电荷密度是电流密度和时间的函数,因此也可以通过实验得到。
人工神经网络(Artificial netural network, ANN)是目前广泛被使用的机器学习方法,可以有效处理输入和输出之间复杂非线性关系。在本文中,神经网络采用了单隐藏层设定,包含20个神经元,隐藏层和输出层的激活函数是sigmoid函数,训练算法是莱文贝格-马夸特(Levenberg-Marquardt)方法,学习率为1×10-6。根据前节中介绍的半循环滑动窗口方法,滑动窗口宽度为2,即包含2个时间步内的数据。每个时间步内,数据类别包括电池电压、面电阻、电池温度、电荷积分、操作电流共5种,因此在1个滑动窗口中一共包含10个数据。以当前时间步的电池电压、面电阻、电池温度和电荷积分(Vt,Tt,ASRt,Qgt)共4个数据作为神经网络的输出,其余6个数据(Vt-1,Tt-1,ASRt-1,Qgt-1,It-1,It)作为输入,输入输出共同组成1个样本,因此神经网格结构为6-20-4。除了基于神经网络耦合半循环滑动窗口方法的数据驱动模型(Nerual network coupling semi-recurrent sliding window model, NN-SW model)外,还考虑了其他机器学习方法如线性回归(Linear regression,LR)耦合半循环滑动窗口方法模型(Linear regression coupling semi-recurrent sliding window model, LR-SW model)的应用。
在数据驱动模型应用于实际预测之前,有必要对模型的泛化能力进行评估和验证。图5展示LR-SW和NN-SW模型的测试数据和预测结果之间的比较。值得注意的是,验证的数据来自案例7和案例10(图3中的红色实线),这两个冷启动过程的初始温度、加载电流速率和启动结果均不同。如图5所示,在电压和面电阻预测方面,NN-SW模型预测效果更好;在温度和电荷密度预测方面,两个模型预测结果基本一致。均方根误差对比显示,在电荷密度方面,LR-SW模型比NN-SW模型更准确,但考虑到电荷密度的数值范围,该准确度的优势可以忽略。考虑到多个变量参数范围接近零值,平均相对误差无法反映目标与预测之间的真实趋势。比较决定系数,发现NN-SW模型(R2 = 0.9927)总体表现优于LR-SW模型(R2 = 0.3875),特别是在面电阻预测方面。虽然两个模型预测温度的决定系数非常接近,但在案例7中LR-SW模型预测电池冷启动将在56 s左右失败,这与实际情况相反。因此,ANN被选为本研究中数据驱动模型的机器学习方法。分别基于神经网络和线性回归数据驱动模型预测结果与真实值之间详细的误差分析结果展示在表2。其中,表格内的每个方框中的数字从左上至右下分别对应的是电池电压、面电阻、温度和电荷密度的误差结果。
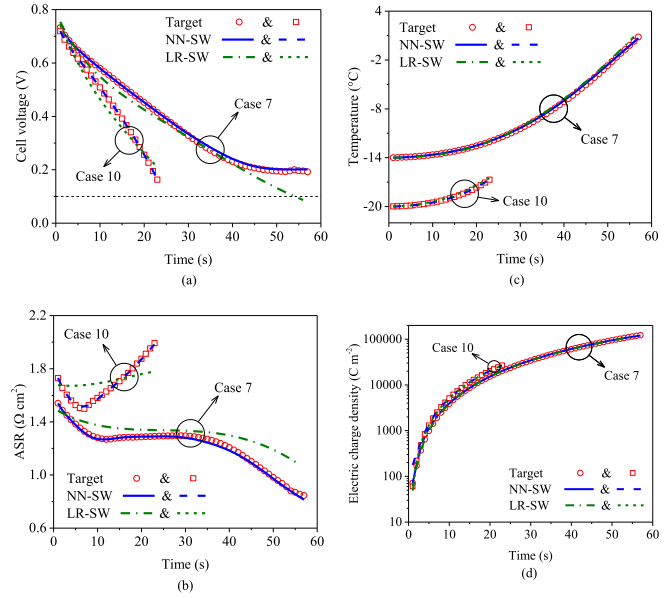
图5 基于神经网络和线性归回的数据驱动模型预测结果和目标值比较:(a) 电池电压;(b) 面电阻;(c) 温度;(d) 电荷密度
表2 数据驱动模型误差分析结果
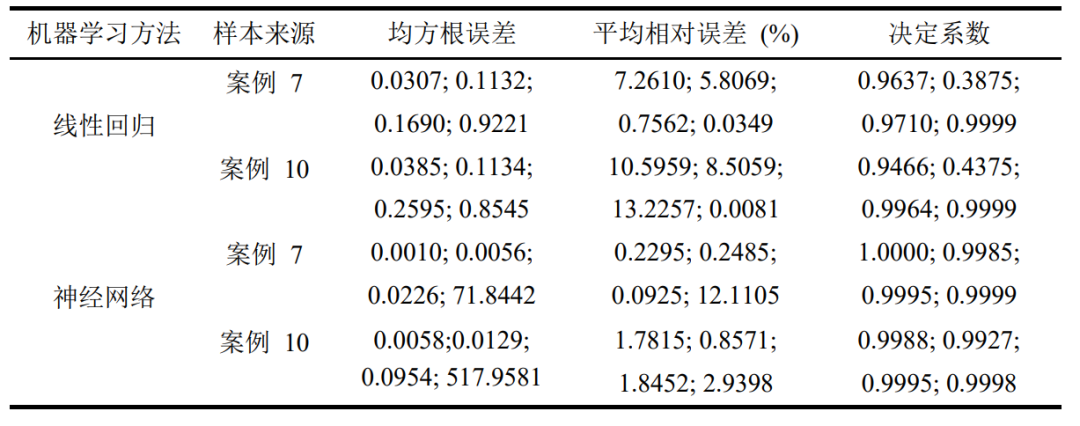
图6展示了根据机器学习模型预测结果,总结了燃料电池低温启动成功的环境温度和电流加载速率MAP图,云图表示启动成功的冷启动持续时间,红色实线表示燃料电池在-20 °C到-8 °C启动温度范围内的最佳恒定电流斜坡工况组合,这也是燃料电池出现电压反极现象的极限边界。该结果显示,根据NN-SW模型,可以通过合理的计算费用和时间成本来实现燃料电池低温启动的精确控制。然而,恒电流加载策略不能完全发挥出燃料电池的低温启动的潜能,因为图6显示的电池电压仍有很大的下降空间。如前研究内容所示,若电池电压越接近安全电压(0.10 V),则冷启动过程中电池加热功率就越大。为了缩短低温启动时间或在较低的初始温度下提高电池的冷启动能力,应进一步优化恒电流加载策略。
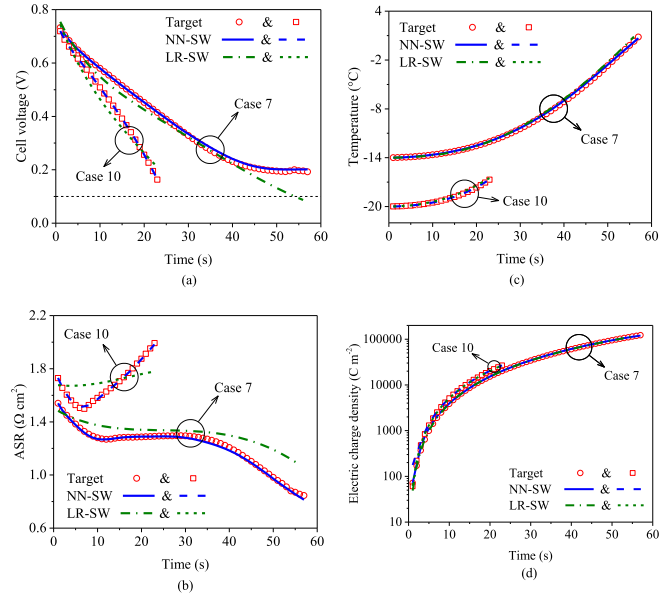
图6 基于恒电流加载速率策略的启动温度-控制条件-启动时间MAP图
在恒电流加载策略基础上,进一步提出实时自适应控制策略(Real-time adaptive control strategy, RACS),该策略在NN-SW模型的帮助下,针对电池-20 °C冷启动困难的问题,实时进行操作条件的优化,缩短电池的低温启动时间,提高电池的低温启动能力。图7显示实时自适应控制策略的逻辑流程图,该策略可以针对电池当前状态,对未来运行电流密度控制做出实时响应,尽可能短的启动时间和实现电压最低安全保护是自适应控制策略的两个主要目标。该策略基于NN-SW模型的快速预测能力,以当前时间步电池的状态,检查未来时刻施加操作条件的影响,将电压和温度的预测结果通过判断作为反馈修正操作条件。由于数据驱动模型高计算效率,此“预测-判断-反馈”过程可以在短时间内重复多次,直到找到合适的操作电流密度,使预测电压维持在安全电压之上,最终实现电池冷启动闭环控制。
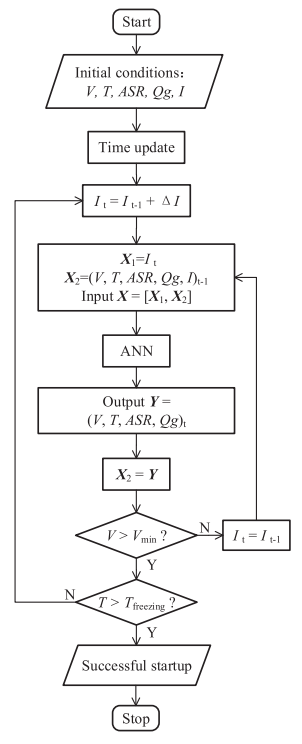
图7 实时自适应控制策略逻辑图
基于实时自适应控制策略,图8 (a)显示分别使用原始恒电流加载速率策略(恒定电流斜率:150 A m-2 s-1)和使用优化后的启动策略的燃料电池,从初始温度-20 °C条件下启动的过程。图8 (b)显示原始策略和优化后冷启动过程中操作电流密度变化。按照原始策略启动,在冷启动进行到16.1 s时,输出电压降低到0.10 V,触发电池安全保护机制而导致冷启动停止。而在实时自适应控制策略控制的冷启动过程中,当输出电压即将下降到安全值之下时,实时自适应控制策略会立即停止当前时刻操作电流密度的增加,以避免欧姆损失进一步增加导致输出电压持续下降;随后当电池内部因膜变湿润而导致阻抗减小后,电压开始回升,则电流密度的增长速度控制在最大的150 A m-2 s-1,尽可能使电池更快获得更大的参考电流密度以及更大的产热功率。如此操作,整个冷启动过程中,电池电压可以维持在在安全电压之上的一个较小范围内,保障电池低电压启动的安全性,同时确保电池温度会以最快的速度上升。图8 (c)显示实时自适应控制策略优化的操作条件应用于燃料电池动态模型,验证该策略的可靠性。对比结果表明,由自适应控制策略提出的操作条件以及对应的电池性能和温度变化,与模型预测结果一致,这显示本研究提出的优化冷启动策略框架是可靠、准确的。
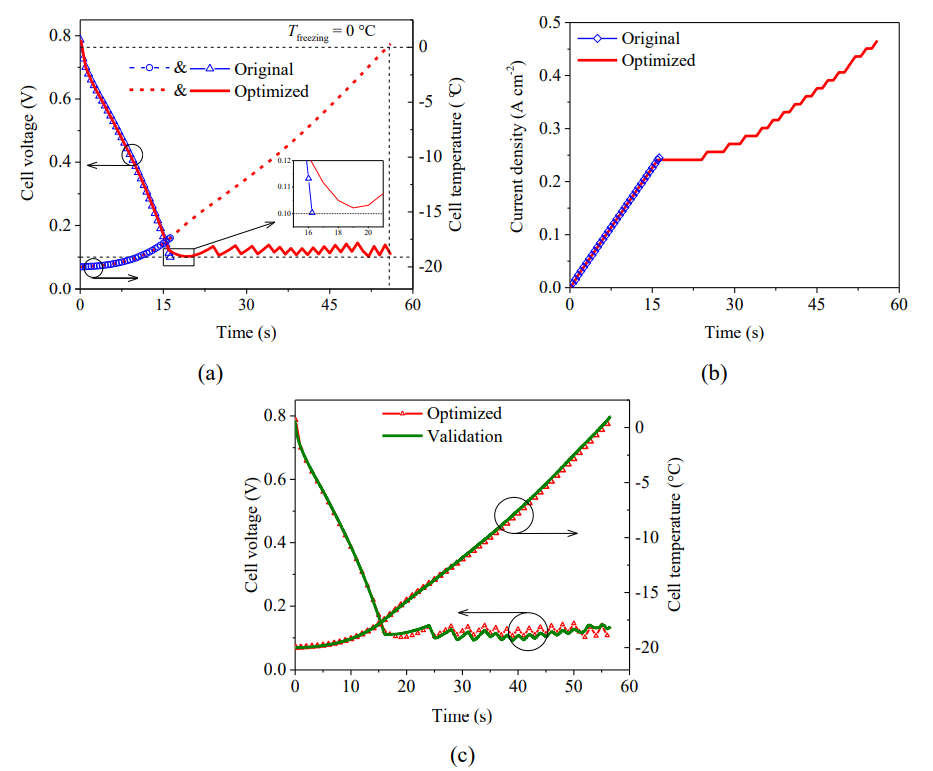
图8 初始-20 °C 冷启动优化操作条件前后对比:(a) 电压和温度曲线;(b) 操作电流密度。(c) 燃料电池模型验证优化后冷启动策略的可靠性
在 NN-SW 模型的帮助下,实时自适应控制策略基于冷启动不同的初始温度条 件,确定优化后的操作电流密度。图9 (a)显示电池在恒电流加载策略下的临界安 全电流密度斜率,而图9 (b)显示对应初始条件下,通过实时自适应控制策略优化后的电流密度控制。
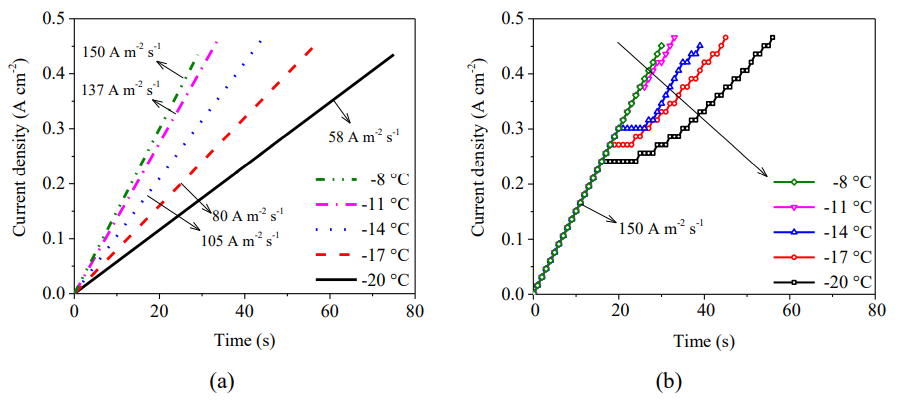
图9 操作电流对比:(a) 恒电流加载速率策略;(b) 实时自适应控制策略
图10 显示原始策略和实时自适应控制策略在不同环境温度下的最佳冷启动时间。可以发现,与原始策略相比,后者可在初始温度较低的工况条件下显著提高电池的冷启动能力。当环境温度从-8 °C降低到-20 °C时,使用实时自适应控制策略优化操作条件的冷启动节省的时间逐渐增多。对于-20 °C的初始温度,优化后的电池启动时间可缩短约26.7%。总而言之,与恒电流加载速率策略相比,自适应控制策略可以有效缩短冷启动时间、实现电池电压最低保护,对于燃料电池冷启动工况而言是更高效、更稳健的控制策略。
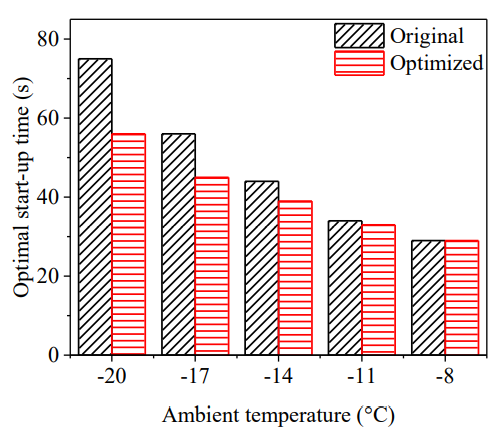
图10 基于实时自适应控制策略优化前后电池最佳冷启动时间对比